Basic Math Aptitude Test

Introduction

Math can be a daunting subject. Most professions don't use math directly. Most workers, however, are more efficacious and confident if they are numerically fluent. Working with numbers, after all, seems to be an inescapable part of any job. And, while computation has become redundant with the accessibility of calculators, you probably won't be too proud having to use a calculator to solve a simple math problem in front of other people.

The good news: when you start practicing mental math regularly and grasp a few basic concepts, you will find that you'll be much better at math than you think you can be. Below are the key areas that will lead to your mathematical success.

Most colleges, including technical colleges, require a basic math course. A 4-year college will require at least one semester of college algebra, while technical/community college will likely require a basic math course, depending on the program. Additionally, certain entry-level jobs may require a basic math aptitude test, including cashier positions, bank tellers, nursing assistants, pharmacy technicians and working as a tutor or paraprofessional in a school setting. In fact, most education positions require general aptitude tests--including one in math--regardless of the field you are teaching. Having competent math skills is your ticket to edging other people out for these positions. Technical/community colleges will have you take some sort of placement test for your math called an Accuplacer. Performing well on these tests may mean that you can pass out of a course--or not taking courses at all, though generally you will need strong algebra skills for the latter.

(Note, this guide is for general math aptitude and is not a guide for the GED, ACT or any other University-entrance exam.)

Arithmetic and Mental Math

This is your ability to complete math problems in your head. To build physical fitness, you need to train and practice. To gain mental fitness, you need to train and practice. The brain and the body like to adapt quickly. Practicing consecutive days for even ten minutes will lead to noticeable improvement if you have not already achieved mathematical fluency.

There are two general exercises that most effectively cover every operation in arithmetic:

1) Count to any number, by any number, from any number--both forwards and backwards.

For example, count by 6's up to 75 starting at 3. Next, count backwards from 90 to 0 counting by 3's. If this is challenging, keep at it! Just like a workout, you'll make the most improvements when you continue to challenge yourself.

Additional Practice

1. Count forwards by 8's from 0 to 96
2. Count backwards by 8's from 98 to 2
3. Count forwards by 7's from 5 to 103
4. Count backwards by 7's from 104 to 6

2) Multiply two numbers together (numbers up to 15)

You don't want to memorize your multiplication charts. While it does help with timeliness, it's using the "memory" part of the brain instead of the "problem solving" part of the brain. And, unfortunately, one cannot memorize their way into being good at math. Your speed will grow when you really struggle your way through each problem. And, like with working out, this will get easier after a handful of practice sessions.

Once you start becoming confident in your mental multiplication, practice your division. Being able to go both ways is very important in mental math.

Fraction Concepts

Fraction concepts are parts of a whole. Half of 40, one-third of 30, three-fourths of a dollar are all examples of fraction concepts. These depend on your ability to multiple and divide numbers. If you find some of these challenging, that may be something to practice as well.

Be able to take half of any number up to 200--including odd numbers. This is a common application of fractions that many struggle to do well. Half of numbers like 64 or 88 are easy because they have two even numbers. Numbers like 93 or 137 are a bit trickier because both numbers are odd.

The best trick for these numbers is to break them into numbers you can take half of easily. Half of 99, for example, can be broken down into 80 + 13 (alternatively 80 + 12 + 1). Likewise 137 can be broken down into 120 + 17 (alternatively 120 + 16 + 1).

Additional Practice

1. What is half of 90?
2. What is half of 99?
3. What is half of 199?
4. What is half of 160?
5. What is half of 167?

Draw the Fraction

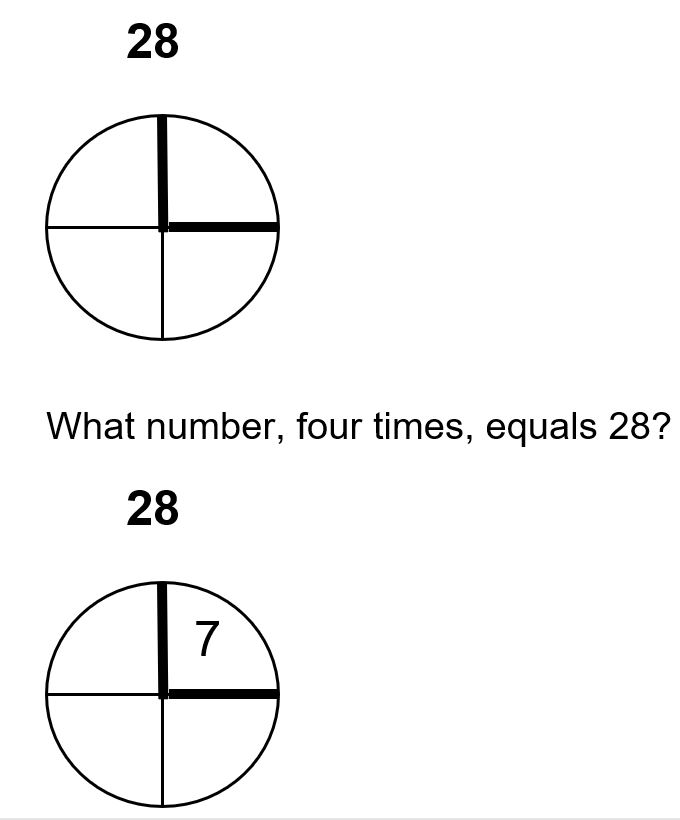
If a fraction problem is hard, drawing it out makes it much easier to think about the steps you need to take to solve it. For instance: find ¼ of 28.

The question is asking us to divide 28 into 4 equal parts, and then take one of them. Drawing it out looks like this:

This image mathematically shows that ¼ of 28 is equal to 7. Likewise, we can use this to know that 2/4 of 28 is equal to 14, and that ¾ of 28 is equal to 21.

Percents

You don't need to do anything crazy, like 11.4% of 326. But, you should be able to take 10, 20 or even 15% of a number that's rounded to the nearest 10. Percent, or per-cent, means per 100. 10% Means 10 out of every 100. If there are 100 bitcoins, and you own 10% of them, that means you own 10 out of the 100 bitcoins.

If 5% of 40 is 2, think about what 15% of 40 is. If the dots are helpful, keep drawing (or picturing them) as you complete these problems. As you practice this, your speed will increase as will your ability to complete these without visuals.

Additional Practice

1. 15% of 40
2. 20% of 50
3. 20% of 70
4. 10% of 80
5. 35% of 80
6. Second Item
7. 12% of 100
8. 24% of 150

Exponents and Roots

In most contexts, these are essentially multiplication problems. Instead of writing 9 x 9, you'll see 9², or nine squared. This is equal to 81. Similarly, 9³ means nine cubed, or 9 x 9 x 9. This equals 729.

When you see a problem like this 4 + 52, you're supposed to perform the exponent operation first. 4 + 5² = 29. However, if you see a problem like this: (4 + 5)², you complete the operation within the parentheses first. (4 + 5)² is equal to 81.

One of the most common applications of exponents is the area of a geometric shape. For instance, the area of a square below is (12 feet)², or 144 square feet.

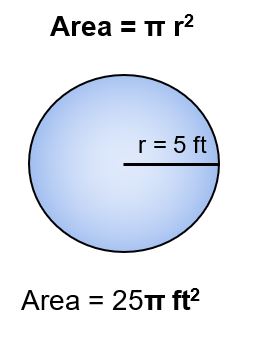
Another area equation is the area of a circle. The area of a circle is found by taking the radius squared and multiplying it by pi.

So how do you find the radius of a circle or the side length of a square if you only know the total area? To find this, you would take the square root of the area. The square root of 144 (√144) is 12, and the √25is 5.

Similar to your multiplication, you should practice learning your square numbers all the way from 12 up to 152.

Additional Practice

1. 12² = _____
2. 10² + 5² = ______
3. (4 + 3)³ = ______
4. √81= ______
5. √((100 + 21))= _______
6. (√((60 + 4)) + √((40-4)))² = ______

Algebraic Thinking

Algebra is built on all of the skills seen up to this point. In short, algebra is math that studies the relationship between two or more variables. How does the cost of a service affect the profit made from that service? Or, how does the number of years of job experience affect a person's salary at a manufacturing company?

Not all examples are this clean-cut, but problems like these help us to see relationships very clearly. The salary at this manufacturing company starts at $45,000 and increases by $3,000 for each year of experience.

An algebraic equation would look something like this:

And the equation would read y = 45,000 + 3,000x. The value of y starts at 45,000 and increases by 3,000 for every value of x. When x = 4, y will equal 57,000. And when x = 5, y will equal 60,000.

Other algebraic expressions will require you to solve for x when given y. For example, using the equation above, how many years will it take for a manufacturing employee to earn $72,000? The equation will look like this:

72,000 = $45,000 + $3,000x

72,000 = ending salary

45,000 = starting salary

3,000 = salary increase per year

x = number of years worked

How much of an increase is it from $45,000 to $72,000? This is the first number we want to find. To do this, we subtract the starting salary, 45,000, from the ending salary, 72,000. This will tell us the increase from our starting salary to our ending salary.

The difference between 72,000 and 45,000 is 27,000. This is how much the salary increased by, over x number of years. Now we just need to find what x is.

9 is the number of years an employee must work in order to earn a $72,000 salary.

Additional Practice

1. In the above example, how many years of experience would it take to earn a $84,000 salary?
2. In the above example, how many years of experience would it take to earn a $100,000 salary?
3. For the equation y = 4x + 8, what will the value of y equal when x is equal to 11?
4. For the equation y = 4x + 8, what is the value of x for the value of y to equal 80?
5. For the equation y = â…” x - 4, what is the value of y when x is equal to 15?
6. For the equation y = â…” x - 4, what is the value of x for the value of y to equal 24?

Conclusion

Building math fitness is very similar to building your physical fitness. You likely won't get the results you're looking for if you do not challenge yourself and if you're not consistent with your practice. Consistency and challenge will bring growth. While challenge is important, it's also important that you are able to understand the math that you are doing. Like with multiplication, you are only getting better at math if you are practicing it--and not memorizing it.